 摘要:
摘要:
美式選擇權是一種允許持有者在合約到期前隨時行使權利的靈活金融工具,其定價複雜性高於歐式選擇權,提供了更多因應市場波動的策略選擇。
美式選擇權是一種特別靈活的金融工具,賦予持有者在選擇權合約到期前隨時行使其權利的自由。這意味著您不必等到到期日,可以根據實際市場狀況隨時做出決策,例如在最有利的時間買入或賣出標的資產。正是這種靈活性使得它在股票選擇權市場上非常受歡迎,但也使得其定價比歐式選擇權更加複雜。
美式選擇權定義
美式選擇權是一種金融衍生工具,賦予持有者在選擇權合約到期日之前隨時行使權利的彈性。持有人可以在選擇權有效期內選擇何時行使買入或賣出標的資產的權利,而無需等待到期日。這種類型的選擇權在股票選擇權市場中被廣泛使用,因為它允許持有者在最有利的市場條件下隨時進行交易。
它包括看漲期權(允許持有人以預定價格買入標的資產)和看跌期權(允許持有人以預定價格出售標的資產)。由於這種靈活性,賣方承擔更大的風險,因此它通常比歐式選擇權稍貴。
美式選擇權的行使規則
它的行權規則允許持有人在合約期限內隨時行使權利,而不必等到到期日。這種靈活性使得投資者可以根據市場狀況、個人投資策略或其他因素的變化來選擇行使選擇權的最佳時機。
首先,它的持有人可以選擇在選擇權期限內的任何一天行使該權利。例如,如果標的資產的市場價格對持有人有利,他們可以選擇立即行使選擇權,無論距離到期日還有多長時間。這種靈活性使投資者能夠更有效地應對市場波動,尤其是當一些市場變化突然且不可預測時。
其次,它的行使通常會受到股利、利率等因素的影響。如果標的資產(如股票)即將派息,且股利會影響資產價格,則持有人可以選擇在派息前行使選擇權以獲得股利。該策略通常與看漲期權一起使用,因為標的股票支付股息後股價通常會下跌。提前行使可以讓持有者規避價格下跌的風險。
此外,美式選擇權適合兩個方向的行使:對於買權,當市場價格高於行使價格時,持有人可以行使以低於市場價格的價格購買標的資產,並獲得價差收入。對於看跌期權,持有人在市場價格低於行使價格時行使選擇權,並以高於市場價格的價格出售標的資產,從而獲利。
持有人在行使選擇權時需要支付執行價格,行使選擇權後所獲得的收益取決於市場價格與執行價格的差額。例如,如果投資者持有執行價格為50 美元的看漲期權,當標的資產價格上漲至60 美元時行權,投資者可以以50 美元購買該資產,並立即以60 美元的市場價格出售。獲得10 美元。
它的靈活性使得選擇權的定價變得更加複雜,因為賣方需要應對選擇權隨時可能被執行的風險。這種風險導致選擇權的定價通常高於歐式選擇權,因為它的為持有者提供了更大的自主權和更具策略性的選擇。
美式選擇權的定價方式
美式選擇權的定價更為複雜,因為它允許持有者在到期前隨時行使權利,這增加了選擇權價格計算的不確定性。與可以使用Black-Scholes 模型計算閉式解的歐式選擇權不同,它的定價通常依賴數值方法。
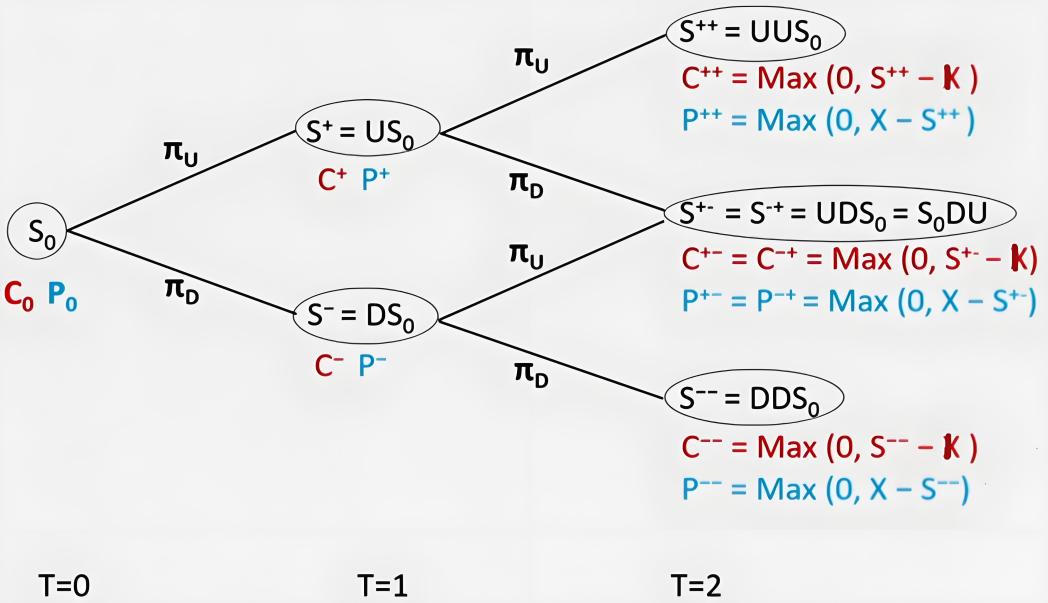
常用的定價方法是二元樹模型。此方法將選擇權的時間劃分為多個小時間段。在每個時間段內,標的資產的價格都可以向上或向下波動,然後透過回溯來計算選擇權的價值。
在每個時間點,你都需要考慮是否要提前行使選擇權,並在比較時選擇價值較高的。此方法能夠準確反映它的早期行使特徵。雖然計算量大,但精度高。
另一種定價方法是蒙特卡羅模擬,它透過模擬標的資產價格的多個隨機路徑來估計選擇權的價值。對於美式選擇權來說,這種方法的挑戰是如何處理在任何時間點提前行使選擇權的可能性。
透過引入一些最佳化演算法,例如長極點迴歸演算法,可以更好地模擬這一特性。蒙特卡羅模擬適用於處理複雜的選擇權結構,但計算成本較高,且精確度取決於模擬的次數和路徑。
有限差分法是另一種數值計算美式選擇權價值的方法。它透過離散Black-Scholes 方程式來處理期權定價問題。在每個離散的時間點,計算選擇權的價值,同時考慮提前行使的可能性。此方法計算精度較高,但實現過程較複雜,通常應用於對結果要求準確的場景。
儘管布萊克-斯科爾斯模型通常用於對歐式選擇權進行定價,但對它進行了一些修改,可用於估計價格。透過調整選擇權的理論值並考慮提前行使的機率,可以得到一個近似的價格。這種修正方法雖然無法準確反映早期運動的複雜程度,但提供了相對簡單的估計方法。
它的定價考慮了多種因素,包括標的資產的波動性、無風險利率、股息支付以及提前行使的可能性。由於早期行使選擇權使得美式選擇權的價值普遍高於歐式選擇權,因此其定價模型也比歐式選擇權複雜,需要採用數值方法進行估算。
美式選擇權和歐式選擇權的區別
它與歐式期權的主要區別在於行使時間的靈活性。
它允許持有人在期權合約的整個生命週期內(從購買之日到到期日)隨時行使其權利。這種靈活性使得它的持有者可以根據市場波動選擇最有利的時間提前行使。尤其是當標的資產股利或市場價格波動較大時,提前行使可能會帶來更多收益。
相較之下,歐式選擇權只能在到期日行使,持有人沒有提前行使的選擇權。因此,歐式選擇權持有者只能等待到期日,無法利用市場中期波動進行調整。
由於美式選擇權的靈活性和定價相對複雜,賣方承擔較大的不確定性和風險,因此它的價格通常略高於歐式選擇權的價格。歐式選擇權的定價相對簡單,特別是使用Black-Scholes 模型來計算閉式解,而美式則需要更複雜的數值方法來定價。
行權時間的彈性是它們的核心差異。前者允許持有人在到期日之前的任何時間行使選擇權,而後者只能在到期日行使選擇權。
美式選擇權以其靈活的行使機制,為投資者提供了更多的策略選擇和應對市場波動的機會。然而,這種靈活性也意味著更大的定價複雜性和潛在風險。
投資時,了解它的特點及其與歐式選擇權的差異可以幫助投資者做出更明智的決策並更有效地管理其投資組合。無論您是利用它的靈活性,還是掌握其定價機制,關鍵是要深入分析市場動態,根據個人投資目標做出適當的選擇。
| 類別 | 描述 | 範例 | 相關因素 |
| 特點 | 隨時行使 | 價格上漲時行使 | 市場波動 |
| 行使彈性 | 有效期限內行使權 | 股利前行使權 | 股息、利率 |
| 定價複雜性 | 使用數值方法 | 二元樹模型 | 波動性 |
| 歐式對比 | 美式隨時行使,歐式僅到期 | 美式選擇權靈活 | 風險管理 |
| 投資決策 | 理解特點,優化策略 | 靈活運用 | 投資管理 |
【EBC平台風險提示及免責條款】:本資料僅供一般參考使用,無意作為(也不應被視為)值得信賴的財務、投資或其他建議。

VOO ETF涵蓋500檔美國頂尖公司股票。 2025年市場看好Loews、Charter通訊、Salesforce、Fair Isaac和Moderna五支成分股的上漲潛力。投資可將VOO作為核心持股再結合潛力股平衡。
2025年08月22日
無人機概念股在2025年成為投資人關注的熱點。台股漢翔、雷虎、長園科等主要聚焦於產業鏈中上游;美股概念股則較集中在整機整合商和系統解決方案巨頭,兩者各具投資機會。
2025年08月22日
私募股票是上市公司向特定投資者非公開發行新股募資,導致股權稀釋並影響每股盈餘(EPS)。股價走勢取決於公司能否有效利用資金提升獲利,否則可能面臨下行壓力。
2025年08月22日