交易里的神奇公式—凯利公式

相信大多数交易者都听说过「凯利公式」，如果有一笔钱，针对某一次投资来分析合适的投入仓位，我们首先想到的就是凯利公式。

该公式由贝尔实验室的科学家约翰-凯利于1956年最早研究提出，用该公式可以计算出一笔资金投入的投注最佳比例，以使财富增长的预期对数(即几何增长率)最大化。

尽管凯利公式在博彩业和金融界经常被提及，但人们对它的理解却很有限。要知道，若是对其了解不足，导致公式的误用，会给投资交易者的财富带来巨大损失。本篇，EBC金融就带大家来深度科普下「凯利公式」。

我们日常在投资、交易时，时常面临两个基本问题：

如何寻找到期望收益为正的投资机会?

如何确定你的投资/赌注的比例大小?

大多数专业交易者都认为两个问题中，第二个问题是更难的，比如：21点玩家决定在某一手牌上下注的比例，房地产投资者决定在她的投资组合中投入多少资金在房地产领域，以及衍生品交易商决定在新策略中使用多少倍的杠杆。

对于大多数投资者来说，相对于仓位大小和风险管理，寻找投资机会是相对容易的。

有人曾说，一个相对平庸的策略，有了伟大的风控模型，也将变得相当成功;而一个伟大的策略，若是风控模型平庸，也会变得很失败。可见，科学的仓位配比/风控模型对投资交易的重要性。

一个简单的例子

凯利公式常用于在已知赔率和胜率，且期望收益为正的投资情境下;而如果一项投资的期望收益为负，则凯利给出的建议是不下注。

例如，一个玩21点的算牌员，他已知当前的"运行计数"和"真实计数"，即已知下一手牌的赢/输概率为52%对48%。52%的赢钱机会当然很有吸引力，但赌徒更希望知道的是在下一手牌中，他该下注多少资金比例?

他必须在「多下注，以获得更大利润」和「少下注，以减少亏损破产的风险」这两种力量之间取得平衡。

而凯利公式告诉我们，在这两种需求力量之间，存在一个最佳的净资产的投注比例，从而使长期财富达到最大化。

我们可以用不同的赌注大小进行实证实验，看看净资产如何随时间变化。让我们先假设赌徒在每手牌上下注他净资产的1%，下面是他在1000手模拟牌过程中净资产的变化图表：

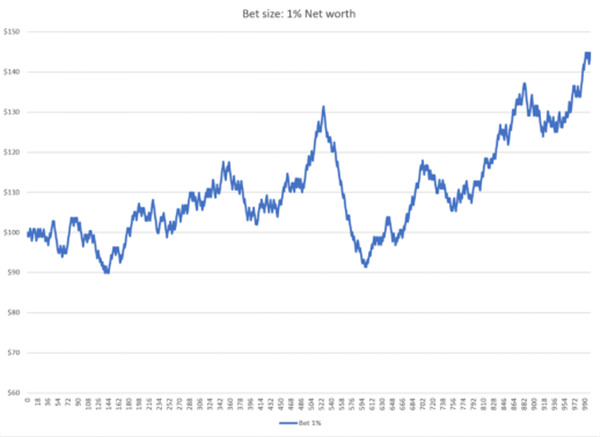
可以看到，这种每次投注1%的策略随着时间的推移会有不错的回报，但也有一定的波动性，1,000手之后，赌徒的财富增加了44%。

如果赌徒在每次下注时下注更大的投资比例(即净资产比例)呢?以下图表是他在每手投入净资产的1%、2%和4%的赌注规模下的长期净资产变化：

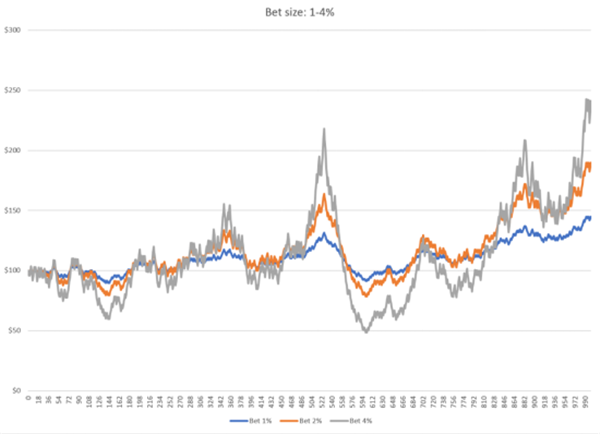
可以很明显地看到，随着赌注比例大小的增加，盈利和净资产的波动性也在同向增加。

我们继续测试更大的赌注规模：

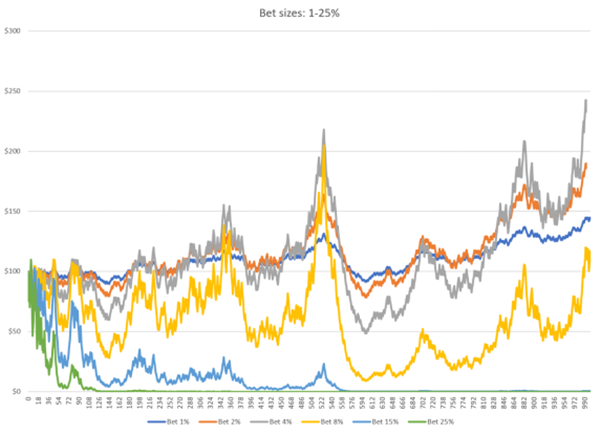
一些出乎我们意料的模拟结果出现了：

虽然我们的累计赢利随着我们的赌注大小从1%增加到4%而稳步增加，但我们看到8%的赌注比例，明显收益更差，15%和25%的赌注比例，甚至使赌徒地的最终净资产为零，即亏光了所有资金。

我们得出结论：随投注比例的增加，净资产变化的波动性会持续增长，但其盈利却是在达到了一个峰值后，出现逆转。所以，盲目的大比例投注，是会对财富产生反向破坏影响的。

这个模拟结果给出了一个衍生思考：在有盈利机会的情况下，为什么多投入，反而会导致更坏的长期结果呢?

数学验证

我们用一个新的例子来探讨，在新的投资项目中，有50/50的收益或损失的机会(即胜率50%)，收益为6%，损失只有5%。你可以选择让你的赌注随心所欲地变大或变小(即使用杠杆)，直至完全损失的可能性。

之前我们用1000个连续的赌注作为长期创造财富的例子。现在，我们将把这个例子简化为2个连续的赌注，一个赢，一个输。因为从长期来看，所经历的赢/输的比例将接近50/50的平均赢/输率。此外，因为我们看的是投资的复合增长，结果的顺序并不重要。因此，考虑2个结果相反的赌注可以合理地估计投资的几何增长率。

以下为初始资金100美元，在不同的下注比例(杠杆量)下，经历一场赢局(+6%)和一场输局(-5%)后的利润情况：

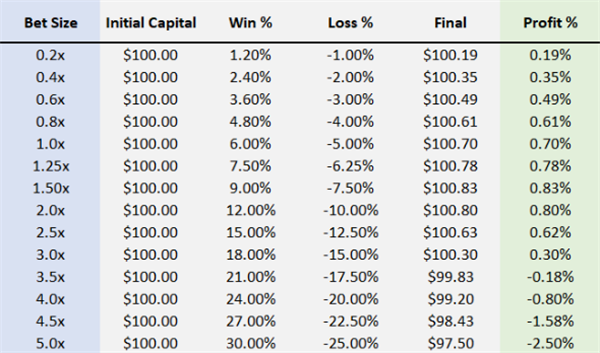
可以看到，在小规模的赌注中，利润随着杠杆率的增加而增长，几乎是一对一的关系。但随着杠杆的增加，利润缩小，最终变成负数。2倍杠杆的利润低于1.5倍杠杆的利润。大于3倍的杠杆率，实际上是一个亏损的策略。

这就让我们引入一个新的概念——NGD(Negative Geometric Drag)，它表示在获得X%的收益后又损失了X%(或先损失后收益)，最终导致的净损失值。例如，如果你在一项投资上损失了10%，然后又赚了10%(投资×0.90×1.10)，你就比最初的投资减少了1%;你先亏损20%，然后赚取20%，你就比开始时减少了4%。

下面是一个胜率为50%，且赢的收益和输的损失相等的投资项目，我们来看下在不同下注比例(即杠杆量)下，NGD的变化：

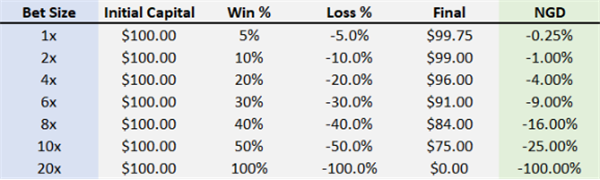
可以看到，NGD的增长速度是杠杆倍率增长速度的平方。

现在我们可以对杠杆如何影响利润有一个更完整的认识，即：

当杠杆增加时，净资产增长的边际利润随杠杆量的增加而线性增长，但在多次投注的场景下，NGD则是随杠杆增长，呈现平方式的增长。

在较低的杠杆水平，边际利润是主导力量，NGD可以忽略不计。然而，随着杠杆率的增长，NGD变得更大，最终压倒了我们的边际利润。

接下来，我们回到胜率50%，收益6%/损失5%的投资项目，在不同的杠杆水平下，边际利润、NGD，以及最终利润的变化：

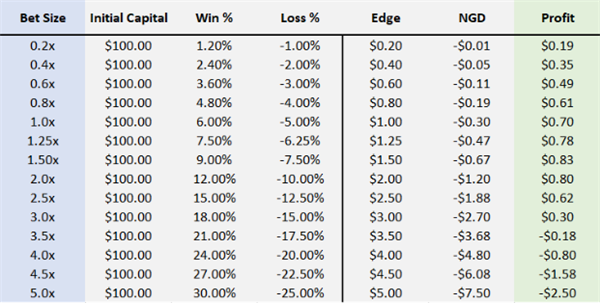
边际利润+NGD=最终利润

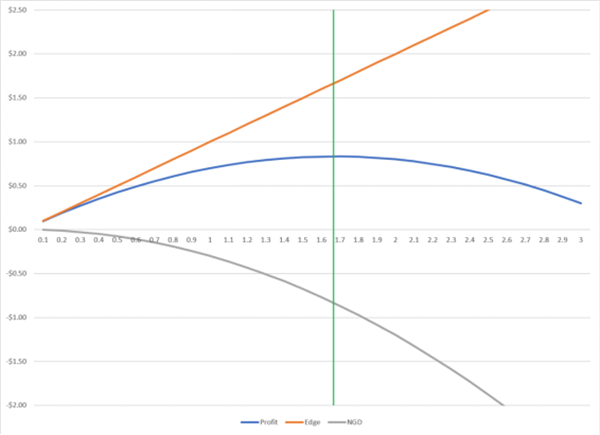
如上图，绿色的垂直线表示边际利润与NGD的两种反作用力完全相互抵消的地方(边际利润=NGD)，这便是最大的利润点(杠杆1.66倍)，任何额外的杠杆都会导致利润下降。

换句话说，使用这个水平的杠杆将使你的财富在多次投注、投资或交易过程中的几何增长率最大化。

以21点的例子为例，在1000次赌注中进行这个实验，1.66倍的杠杆将把100美元变成大约6340美元。3倍的杠杆仅能返回447美元，而4倍的鲁莽杠杆将把原来的100美元磨成不到2美元。

凯利公式

在探讨了上述杠杆的正、反作用后，我们来讨论凯利公式。

凯利公式，旨在已知胜率，和预期盈亏的情况下，推算出每次可以投入的净资产比例，以实现最大的财富增长速度。

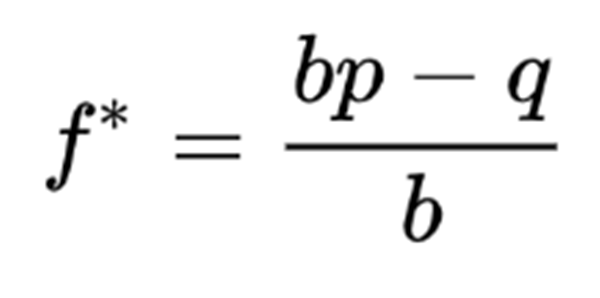
上述方程的左边，f*，是我们应该投入风险的总财富的百分比。

在右手边，p是赢的概率，q=1-p是输的概率，b是赔率(即我们赢的金额与我们输的金额的比率)。例如，如果我们要么赢2美元，要么输1美元，我们的赔率是2:1，我们将b设为2。

将凯利应用于我们的投资实例：

p = 50%，q = 50%，b = 1.2

在这种情况下，我们设定b=1.2，以表示赢钱的报酬(6%)是输钱的惩罚(-5%)的1.2倍。然后我们可以将这些数值填入公式中：

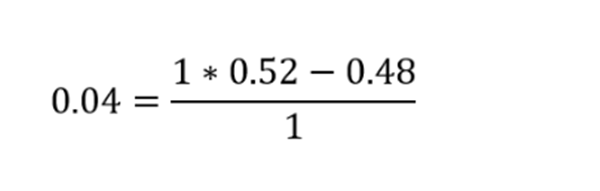
经过凯利公式计算得到，下注的最优选项是总财富的8.33%。由于我们例子中的基本损失是5%，这意味着我们应该使用8.33%/5%=1.66的杠杆。这正是我们之前发现的数值。

再来看21点的例子，打牌的人有52%的机会赢钱(p)，48%的机会输钱(q)，赔率是平的(b=1)。

经过凯利公式计算得到，应该投注其资产的4%。

重新审视上面的图表，我们可以看到，凯利公式正确计算了两种情况下的最佳赌注。

接下来，EBC金融将进一步给大家介绍凯利曲线。

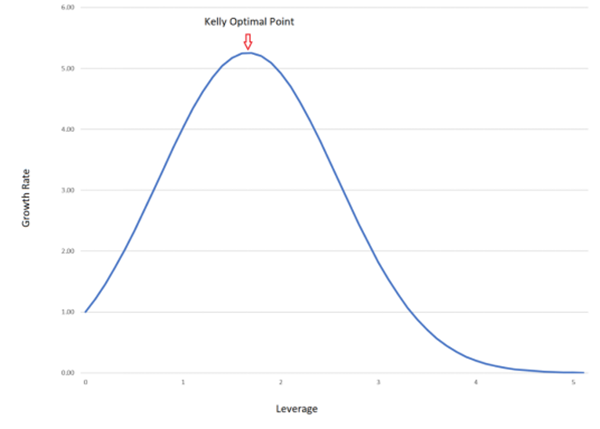
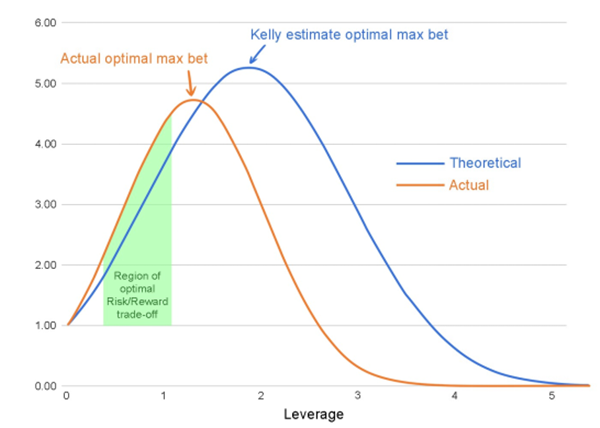
上图中，Y轴代表几何增长率，X轴代表杠杆率，凯利最佳赌注位于曲线的最高点。其实在很多领域的实践应用中，图表所展示的形态一般都是相似的。

凯利公式主要应用的场景，是在已知胜率和已知报酬(即赔率)的情况下，可以推算得出应该投注的资金比例，以实现资产的最大增长。

但需注意的是，凯利公式并不能用来计算投资取胜的概率和盈亏的回报率。

凯利公式代表了理性赌注范围的极限，比凯利公式得出的结论多下一分钱的赌注都会带来风险的增加，即所谓方差增加的同时，利润却在减少。

然而，在大多数情况下，当投注量接近凯利最佳点时，凯利曲线的陡峭度会减缓，意味着额外的风险与额外的利润之比会达到无穷大，就表示投资者可能会多冒10亿美元的风险来赚取多一分的预期利润。

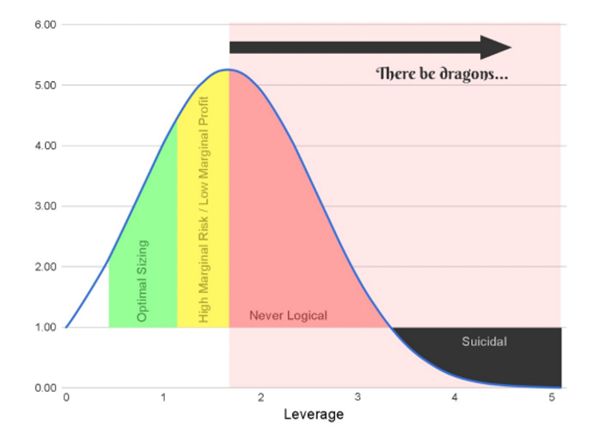
结合上图，绿色区域是相对更优选的开仓比例，特别对于规避风险的投资交易者来说。

理论与实践

「在理论上，理论和实践之间没有区别。但在现实实践中，却有。」

为了在现实实践中利用凯利公式，这里提出两项修正：

1、对拟投资项目的假设要尽可能保守，从各种可能的情况中选取最坏的情况(胜率、赔率)，在用凯利公式计算赌注之前，给你的投资预估打上严谨的保险。

2、对凯利公式计算出的仓位比例，设置一个的打折系数(可以是0.3倍或0.5倍)。

第1项修正是考虑到公式中使用的盈利概率和赔率只是估计。真正的概率和回报是隐藏的，十有八九，现实中的盈利会比我们预估的要少。当在一个不确定的世界中投资时，保守的假设比预期更接近现实。这就是所谓的「安全边际」。

第2项修正来自于以下的观察结论：

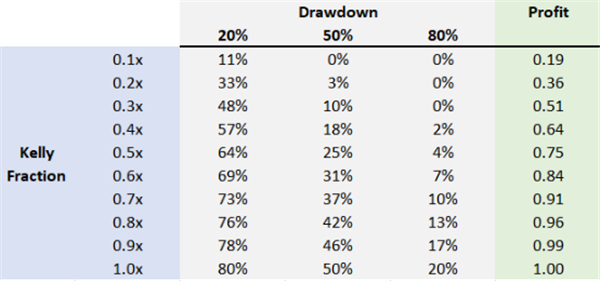
相对于凯利公式计算所得的仓位，乘以打折系数，可以一定程度减少波动性风险(方差)，且相应期望收益的减少幅度要小于方差，如上表所示。所以，以0.3倍或0.5倍凯利仓位的大小下注，可以保留不成比例的预期利润。具体来说：

下注50%的凯利仓位比例，可以获得凯利最佳利润的75%，但是只承担了1/4的方差(波动性风险)。

下注30%的凯利仓位比例，可以获得凯利最佳利润的51%，但是只承担了1/9的方差(波动性风险)。

对于一般个人投资者，30%的凯利仓位比例，是非常合理且可接受的;而对于专业投资者，或是从事代客理财资金管理业务的投资者来说，最佳风险管理/仓位水平甚至更低，特别是在下游客户需求多变的情况下，这时对于资金管理者来说，如何保持投资交易的稳定是首要法则，一般选择的打折系数是凯利仓位的0.1倍-0.15倍。

结语

凯利公式在投资交易中有着非常广泛的应用，它的核心是控制风险，并在此基础上，实现收益的最大化，它是人类理性交易的代表。最后，总结几点凯利公式的精髓：

1、 当投资项目期望收益为正时，凯利公式可计算出在交易者免于破产的情况下，最快速增加资产的投注比例。

2、当投资项目期望收益为零或负值时，停止下注。

3、当期望收益相同时，提高交易系统的胜率或赔率，则可相应提高最大仓位，继而提升资产增长率。

4、凯利公式应用于各类投资交易时，由于市场状态的不同，不能使用过于激进的凯利公式计算仓位，可设置一定的打折系数，以降低交易风险。