道指（US30）&标普500（SPX）背离，有套利机会吗？

做美股指数交易的投资者们，一定对道指、标普指数不陌生，我们从其走势图上，不难看出二者在长期走势上存在趋同一致的属性：

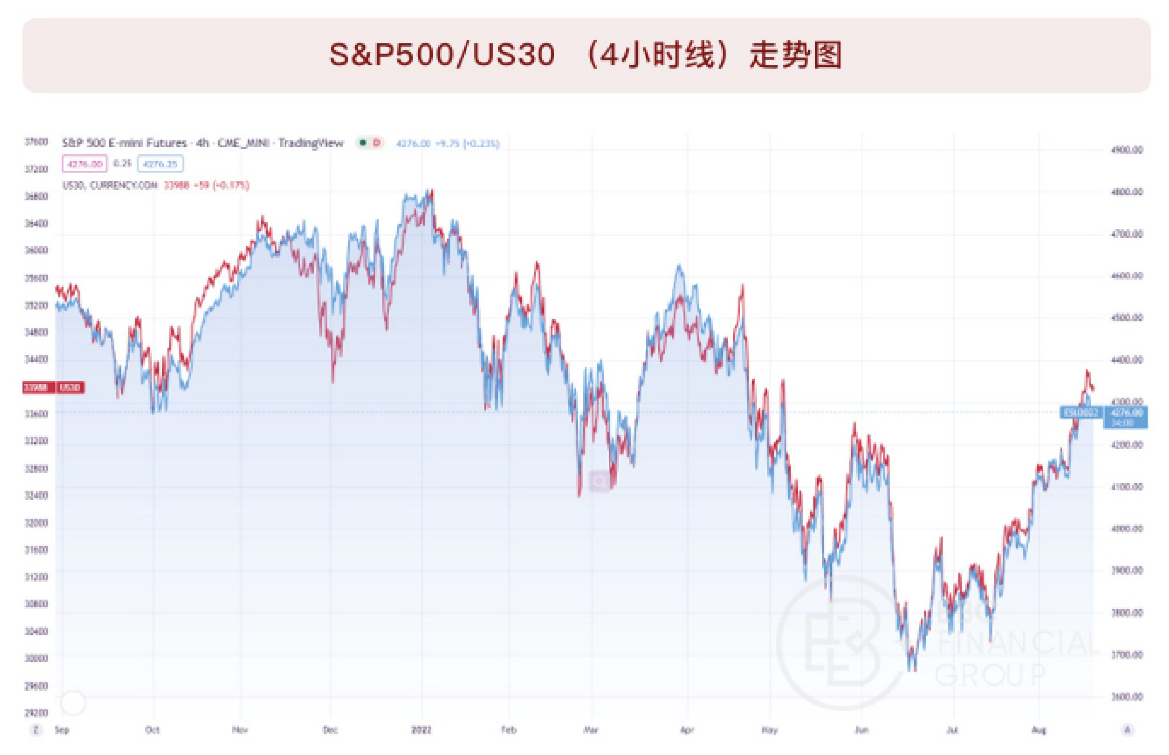
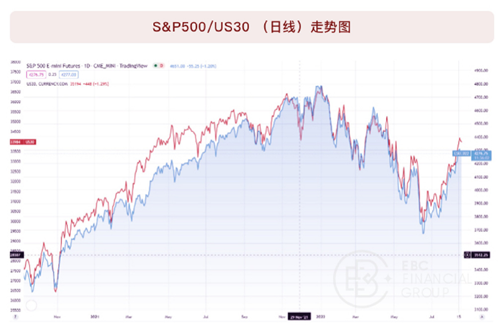
可以看到，U30道指和SPX标普指数，无论在4小时线，还是日线上，均呈现长期一致的走向，特别是4小时线，二者几乎可以重叠。

据此，是否可以通过寻找二者短期内的背离，抓取套利机会呢?本期EBC研究院，就从数据量化视角，带大家一起寻找「交易机会」。

道琼斯指数

道琼斯指数最早在1884年由道琼斯公司创始人查尔斯·亨利·道(Charles Henry Dow)提出，它主要编制的是一种算术平均股价指数。

而我们通常所提及的道琼斯指数是指道琼斯工业平均指数(Dow Jones Industrial Average)，亦称US30，其由美国30家最具代表性的工商业公司股票组成，是美国蓝筹股的代表。

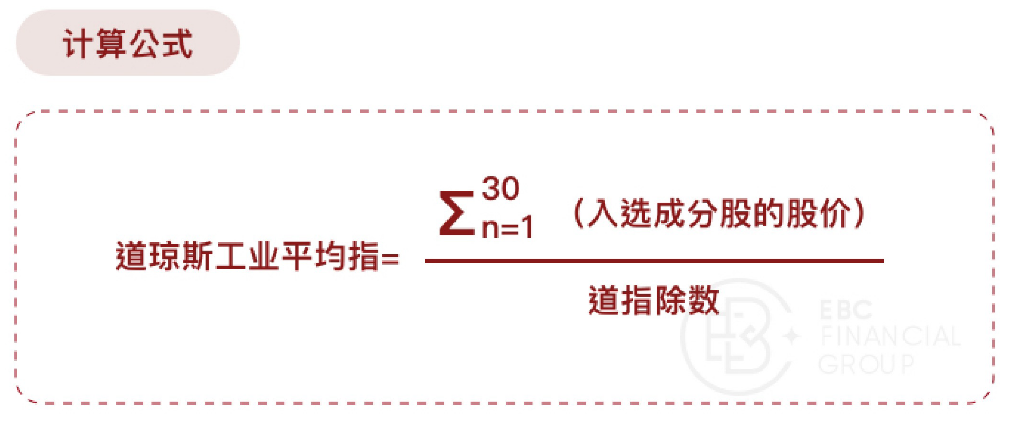
道指除数：1928年9月，道琼斯开始用经过复杂的公式调整的"除数"取代原来的股票总数，来校正股票分拆和公司并购的影响，经多轮拆股后，道指除数约为0.1458。

标准普尔500指数

标准普尔500指数(S&P 500 Index)是由标准·普尔公司1957年开始编制的，是记录美国500家上市公司的一个股票指数，其成分股由400种工业股票、20种运输业股票、40种公用事业股票和40种金融业股票组成。

与道琼斯工业平均股票指数相比，标准普尔500指数具有采样面广、精确度高、连续性好等特点。

市值加权：标普500指数以1941年至1943年为基期，采用加权平均法进行计算，以入选成分股的每只股票上市市值为权数，按基期进行加权计算。公司的市值规模越大，它在标普500指数中的权重就越大。

本篇，我们选取2021至2022上半年，道指(US30)和标普(S&P500)指数4小时线的走势数据，得到二者走势比对如下：

可以较直观地看到，二者走势较为趋同。

接下来，我们对两组数据做相关性检验，得到结果如下：

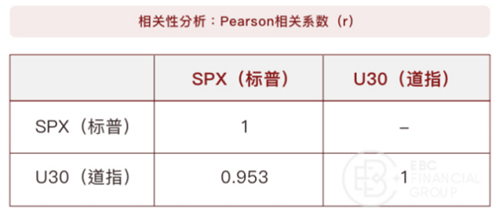
Pearson相关系数，常用字母r表示，用于度量两个或多个变量间的关联程度，其值介于【-1，1】之间，取值为正，代表正向(同向)相关，取值为负，代表负向(反向)相关。一般情况下，相关系数的绝对值大于0.7，即代表具备较强的相关性。

据上表，道指(US30)和标普(SPX)的Pearson相关系数为0.953，表明二者显著性相关。

为进一步量化比对二者之间关联关系，我们选取二者倍率(“US30道指”除以“SPX标普”)作为观察对象，计算数据以每根4小时线的收盘价为准。2021至2022上半年，(US30道指/SPX标普)倍率变化趋势如下：

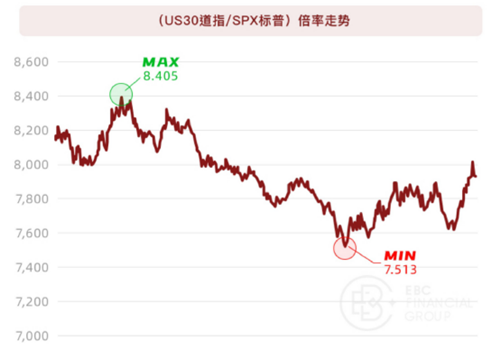
如上图，倍率基本在7.5—8.5之间徘徊：

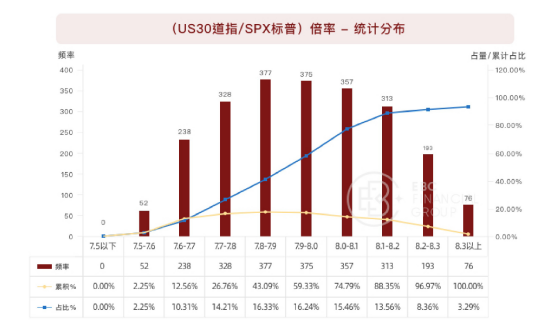
我们进而对倍率的概率分布进行统计，得到(US30道指/SPX标普)倍率分布如下：

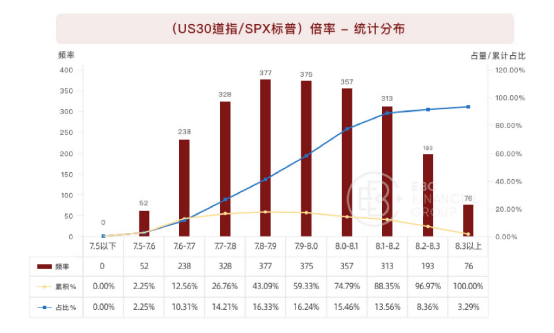
注释：

上图横坐标表示各倍率分布区间;

【频率】表示(“US30道指”/“SPX标普”)的倍率数值，落在各倍率分布区间内的样本个数;

【占比】表示各倍率分布区间内，对应“频率”个数除以总样本数;

【累计占比】表示对应各倍率分布区间，之前所有倍率分布区间的累计“频率”个数除以总样本数。

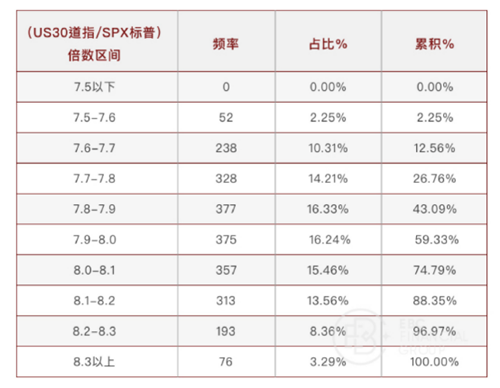
根据倍率统计分布图来看，(US30道指/SPX标普)倍率呈现较为明显的“正态分布”，为检验该正态分布的有效性，画出Q-Q-Plot：

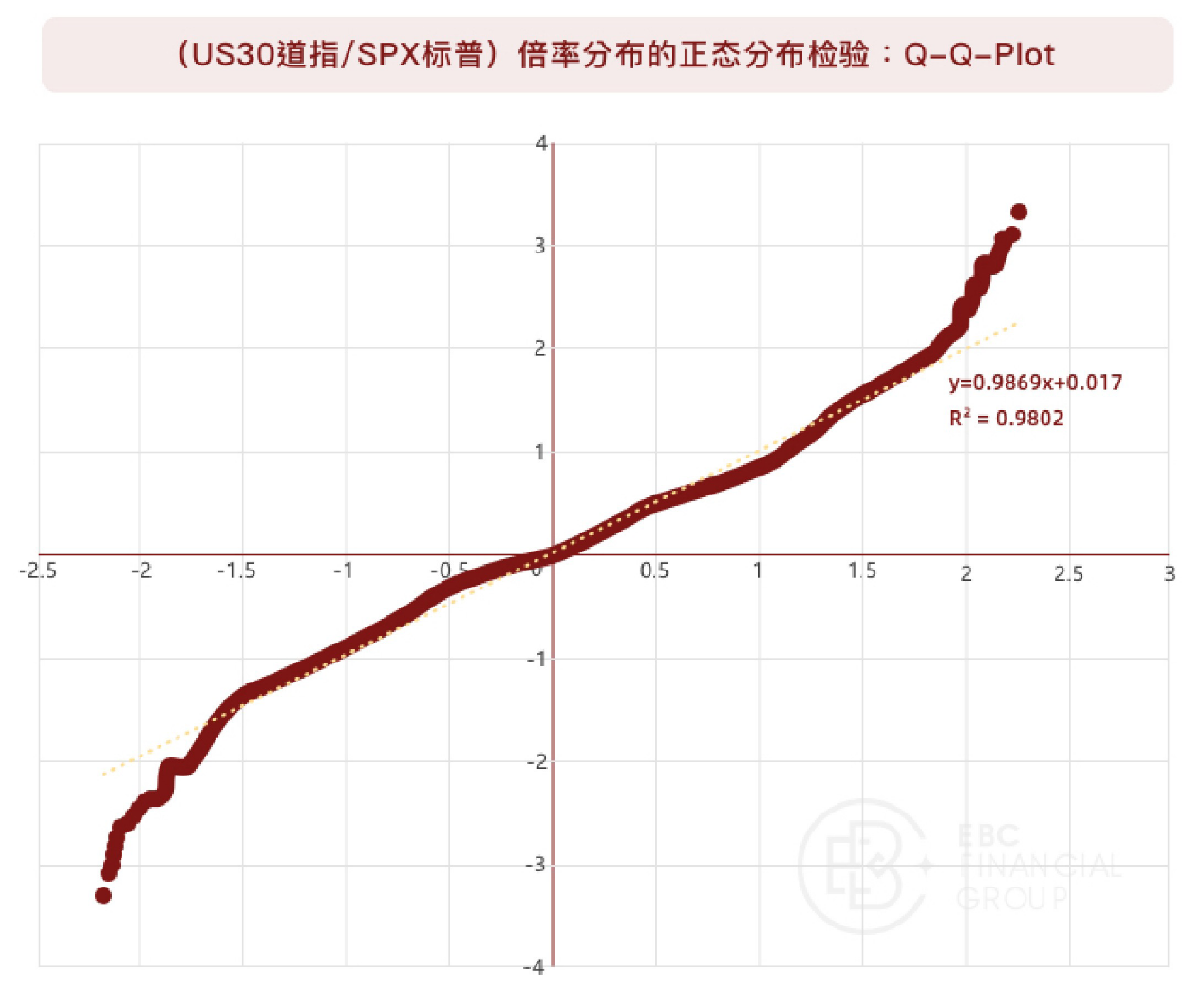
什么是Q-Q-Plot?

Q-Q-Plot全称Quantile-Quantile Plot，这里的Q代表quantile, 分位数的意思。

分位数，也称之为分位点，最常见的有中位数，四分位数等。以中位数为例，将数据集从小到大排列后，50%区域对应的点就是中位数。同理，四分位数分别对应25%， 50%， 75%， 依次称之为第一四分位数，第二四分位数，第三四分位数，其中第二四分位数就是中位数了。

分位数可以很好的展示数据从最小值到最大值的跨度变化，在分位数点取值足够多的情况下，就可以用来代表整体数据的分布情况。

Q-Q plot就是基于上述原理，分别计算得到两组数据的分位数，然后绘制散点图：

如果两组数据分布总体完全一致，其Q-Q plot是一条y=x的直线;

如果两组数据符合同一分布，则其分位数应该符合线性关系。

回到本例，为检验(US30道指/SPX标普)的倍率分布是否符合正态分布，上图Q-Q-Plot中：

我们横坐标选取2021至2022上半年US30道指和SPX标普500指数的4小时收盘数据，以(US30道指/SPX标普)倍率为观察样本，做标准化处理后，得出分位数值;纵坐标选取标准正态分布对应的分位数值;画出二者散点图，得到拟合模型如下：

什么是R² ?

R²又名”R-Square“，其取值范围在【0-1】之间，在统计学中，R²越接近1，代表统计模型的拟合度越精确。

可以看到，二者符合标准线性关系，且R²高达0.9802，表明模型拟合度较优;

据此，则可认为(US30道指/SPX标普)倍率呈现较典型“正态分布”，符合正态分布的相应规律。

正态分布

「正态分布」来源于人类通过观察所得到的自然规律，社会中的有许多变量当达到一定数量后，均可呈现以平均值为中心，两端分布对称的正态分布的趋势，例如：人类身高、出生体重、学生成绩等，所以在自然科学、医学、金融学等很多领域中的量化统计，均是基于正态分布的假设。

标准差

「标准差」表示的是一组变量数据的波动程度(即波动率)，往往以数组平均值(μ)作为参照，数据围绕平均值的波动程度即可由标准差(σ)反映出来。

在正态分布中，围绕平均值(μ)的两端，变量数据总体呈现左右对称的分布形态。

“68-95-99.7”关联法则

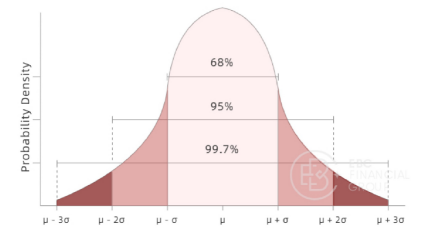
如上图，是一组正态分布数据的概率分布，其中μ为平均值，σ为标准差

横轴表示数据值，纵轴表示每个数据值对应发生的概率(在统计学中称为概率密度)

我们可以很直观地看到68%、95%、99.7%代表的是面积占比(在统计学中称为概率分布)，其实际意义是：

【道指(US30)/标普(SPX)倍率】的均值μ/标准差σ

依据2021至2022上半年4小时收盘数据，(US30道指/SPX标普)倍率取值分布如下：

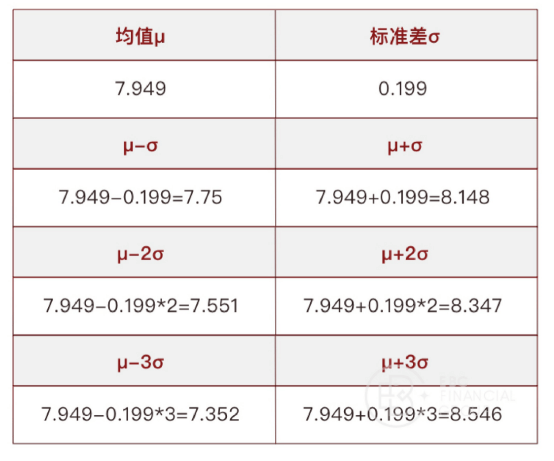
经统计，(US30道指/SPX标普)倍率的均值、标准差如下：

参照上述正态分布的相关规律，得(US30道指/SPX标普)倍率的发生概率如下：

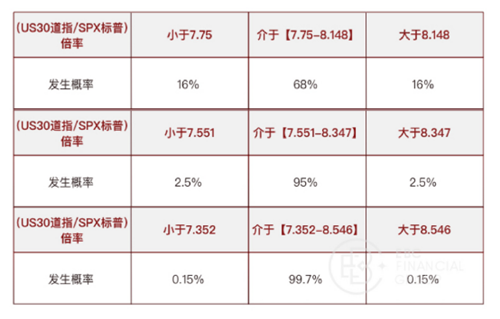
据此，若道指(US30)和标普(SPX)走势出现背离，交易者可计算出当下(US30道指/SPX标普)倍率的取值，结合上表，判断其所在的发生概率区间，若处于发生小概率区间，则可进行「套利交易」。

应用举例

假设当前道指(US30)32920点，标普500(SPX)为4360点

则(US30道指/SPX标普)=32920/4360=7.55

结合(US30道指/SPX标普)倍率发生概率表：

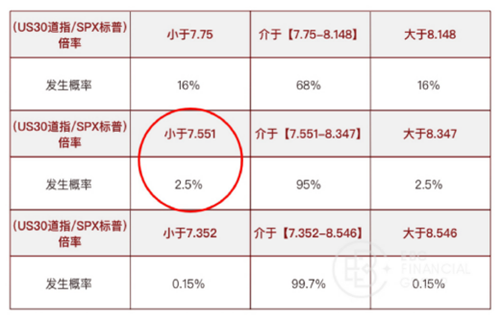
据上表，7.55属于【小于7.551】倍率区间，该倍率数值属于发生概率在2.5%以下的情况，后续返回正常倍率区间的可能性极高;

故交易者可结合当下行情：

如遇道指大幅下跌，导致道指偏低;或是标普500大幅冲高，导致标普指数高估;

可做相应套利交易。

*统计数据基于历史行情，不代表未来表现，统计结果仅作为交易参考，不构成任何投资建议。